黎曼曲率
现在我们来关注黎曼曲率。总的来说,黎曼曲率提供了一种方案,让身处空间内部的人也能计算自身所处空间的弯曲程度。俗话说,“不识庐山真面目,只缘身在此山中”,还有“当局者迷,旁观者清”,等等,因此,能够身处空间之中而发现空间中的弯曲与否,是一件很了不起的事情,就好像我们已经超越了我们现有的空间,到了更高维的空间去“居高临下”那样。真可谓“心有多远,路就有多远,世界就有多远”。
如果站在更高维空间的角度看,就容易发现空间的弯曲。比如弯曲空间中有一条测地线,从更高维的空间看,它就是一条曲线,可以计算曲率等,但是在原来的空间看,它就是直的,测地线就是直线概念的一般化,因此不可能通过这种途径发现空间的弯曲性,必须有一些迂回的途径。可能一下子不容易想到,但是各种途径都殊途同归后,就感觉它是显然的了。
怎么更好地导出黎曼曲率来,使得它能够明显地反映出弯曲空间跟平直空间的本质区别呢?为此笔者思考了很长时间,看了不少参考书(《引力与时空》、《场论》、《引力论》等),比较了几种导出黎曼曲率的方式,简要叙述如下.
求导顺序不能乱
一般的张量分析或者黎曼几何教材中,导出黎曼曲率的方式是考虑二阶协变导数顺序的差别: \[\begin{equation}\label{eq:reimann0} A^\mu_{;\alpha;\beta}-A^\mu_{;\beta;\alpha}=-R^\mu_{\nu\alpha\beta}A^\nu \end{equation}\]
由此可以分离出黎曼曲率张量\(R^\mu_{\nu\alpha\beta}\)来,这确实是一种爽快的途径,但它的几何意义并不明显,很难看出它是怎么反映空间是曲还是直的。而且我们现在还没有定义二阶协变导数(一次协变导数后有两个指标,即相当于一个矩阵而不是向量了,定义高阶协变导数需要细节上的跟进),而这个定义基本上是纯粹代数演算,目前对我们来说意义不大,因此我们这里不作定义,读者直接参考教材即可,所以我们也不对这种方案多作讨论。
在弯曲空间邂逅
此外,还有通过测地线偏离(在广义相对论中对应于潮汐力)来导出黎曼曲率的,那也算是一种几何意义和物理意义都很明确的方案,但是涉及到的计算比较繁琐。主要思路是:考虑测地线方程 \[\begin{equation}\label{eq:cedixian0} \frac{d^2x^\mu}{ds^2}+\Gamma^\mu_{\alpha\beta}(x)\frac{dx^\alpha}{ds}\frac{dx^\beta}{ds}=0 \end{equation}\] 假设有另一条测地线\(x(s)+\delta{x}(s)\), 那么定满足方程 \[\begin{equation}\label{eq:cedixian1} \frac{d^2(x^\mu+\delta{x^\mu})}{ds^2}+\Gamma^\mu_{\alpha\beta}(x+\delta{x})\frac{d(x^\alpha+\delta{x^\alpha})}{ds}\frac{d(x^\beta+\delta{x^\beta})}{ds}=0 \end{equation}\] 假设\(\delta{x}\)和\(d\delta{x}/ds\)都是无穷小量,两式作差,得到 \[\begin{equation}\label{eq:cedixian2} \frac{d^2\delta{x^\mu}}{ds^2}+\frac{\partial\Gamma^\mu_{\alpha\beta}}{\partial{x^\nu}}\delta{x^\nu}\frac{dx^\alpha}{ds}\frac{x^\beta}{ds}+2\Gamma^\mu_{\alpha\beta}\frac{d\delta{x^\alpha}}{ds}\frac{dx^\beta}{ds}=0 \end{equation}\] 其中\(\delta{x}\)就被称为测地线偏离,在黎曼几何中,称之为“雅可比向量场”。上述形式已经足够简单,然而,我们倾向于写成协变导数的形式,因为协变导数才是在弯曲空间中合理的导数,前面我们已经定义了沿测地线的导数\(\frac{DA^\mu}{Ds}\), 重复一次,我们就能够得到沿测地线的二阶导数\(\frac{D^2A^\mu}{Ds^2}=\frac{D}{Ds}\left(\frac{DA^\mu}{Ds}\right)\), 这是容易办到的,但因为我们这里不是特别关心这种方案,因此就不写出\(\frac{D^2A^\mu}{Ds^2}\)的具体形式了,读者可以自己推导。经过计算后,就会发现 \[\begin{equation}\label{eq:cedixian3} \frac{D^2\delta{x^\mu}}{Ds^2}=-R^\mu_{\nu\alpha\beta}\delta{x^\alpha}\frac{dx^\nu}{ds}\frac{dx^\beta}{ds} \end{equation}\] 这就出现了曲率张量\(R^\mu_{\nu\alpha\beta}\)。从数学来看,非零的\(R^\mu_{\nu\alpha\beta}\)实际上表明了测地线分布的不均匀,这就是弯曲空间的体现之一。
这种方案让笔者想起了几米的漫画作品《向左走·向右走》,说的是男女主角一个习惯向左走,一个习惯向右走,于是他们两个看起来永远不会相遇。但有一天他们在圆形喷水池相遇了——在圆的一端背向行走,最终在圆的另一端相遇了。而在弯曲空间中,比如在球面上,即便两条平行线也有相交的机会。这其实表明,“弯曲”其实更为深刻和有趣,它给予了我们世界更多的可能性。
"溜达"回来的变化
最后还有一种分析向量沿着闭合曲线平移后的变化的方案,我们在这里详细分析它。事实上它跟测地线偏离是等价的,只是它的几何意义更加明显,有助于导出更为深刻的结果。它表明,如果一个向量“溜达”一圈回来之后,它就不一定是原来的向量了。下图的例子就清晰表明了这一点。
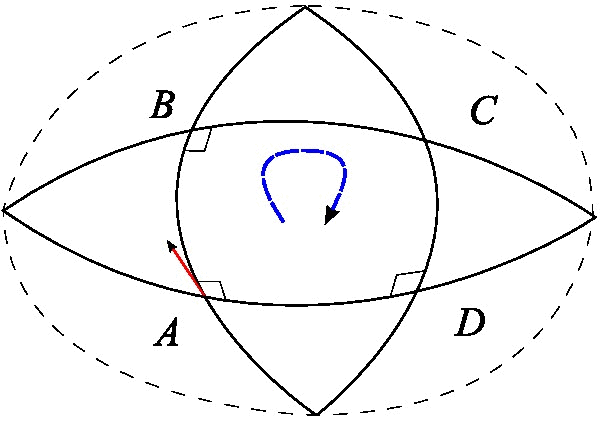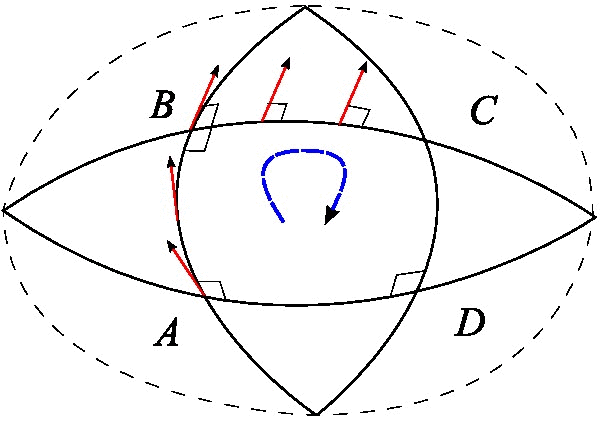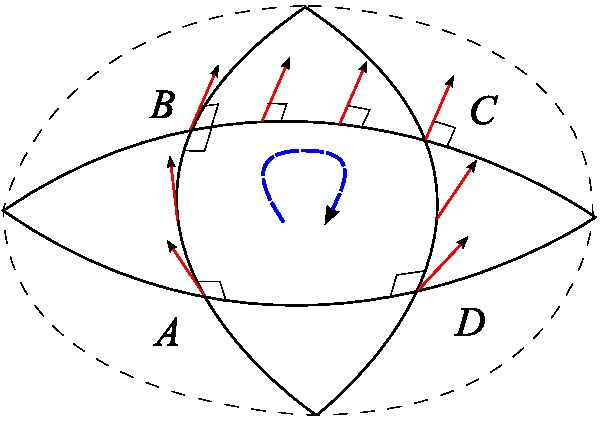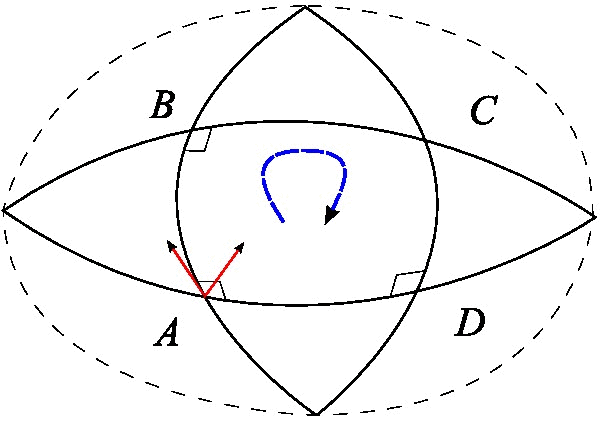
假设\(x^\mu\)处有任意一个向量\(A_\mu\),从\(x^\mu\)出发,先平移无穷小量\(dx^\mu\),再平移无穷小量\(\delta{x^\mu}\),然后再平移无穷小量\(−dx^\mu\),最后平移无穷小量\(-\delta{x^\mu}\),也就是沿着一个无穷小的平行四边形走了一圈,回到原点: \[\begin{equation}\label{eq:cedixian4} x^\mu\to x^\mu+dx^\mu \to x^\mu+dx^\mu+\delta{x^\mu} \to x^\mu+\delta{x^\mu} \to x^\mu \end{equation}\]
我们逐步计算平移过程中\(A^\mu\)的变化,从\(x^\mu\)到\(x^\mu+dx^\mu\),\(A_\mu\)变为 \[\begin{equation}\label{eq:cedixian5} A^\mu-\Gamma^\mu_{\alpha\beta}(x)A^\alpha dx^\beta \end{equation}\] 接着从\(x^\mu+dx^\mu\)到\(x^\mu+dx^\mu+\delta{x^\mu}\), \(A^\mu\)变为 \[\begin{align}\label{eq:cedixian6} A^\mu&-\Gamma^\mu_{\alpha\beta}(x)A^\alpha dx^\beta-\Gamma^\mu_{\nu\gamma}(x+dx)\left[A^\nu-\Gamma^\nu_{\alpha\beta}(x)A^\alpha dx^\beta\right]\delta{x^\gamma} \notag \\ &=A^\mu-\Gamma^\mu_{\alpha\beta}(x)A^\alpha dx^\beta-\Gamma^\mu_{\nu\gamma}(x)A^\nu\delta{x^\gamma}-\frac{\partial\Gamma^\mu_{\nu\gamma}(x)}{\partial x^\beta}A^\nu d{x^\beta}\delta{x^\gamma} \notag \\ &\quad +\Gamma^\mu_{\nu\gamma}(x)\Gamma^\nu_{\alpha\beta}(x)A^\alpha dx^\beta \delta{x^\gamma} \end{align}\] 这里我们只精确到二阶项。类似地,如果考虑路径\(x^\mu\to x^\mu+\delta{x^\mu}\to x^\mu+dx^\mu+\delta{x^\mu}\)所带来的变化,则只需要将\(dx\)和\(\delta{x}\)交换 \[\begin{equation}\label{eq:cedixian7} A^\mu-\Gamma^\mu_{\alpha\beta}(x)A^\alpha \delta{x^\beta}-\Gamma^\mu_{\nu\gamma}(x)A^\nu d{x^\gamma} -\frac{\partial\Gamma^\mu_{\nu\gamma}(x)}{\partial x^\beta}A^\nu \delta{x^\beta}d{x^\gamma}+\Gamma^\mu_{\nu\gamma}(x)\Gamma^\nu_{\alpha\beta}(x)A^\alpha \delta{x^\beta} d{x^\gamma} \end{equation}\] 那么很自然地,路径\(x^\mu+dx^\mu +\delta{x^\mu}\to x^\mu+\delta{x^\mu} \to x^\mu\)所造成的变化就是上式的相反数。于是,整条闭合路径\(x^\mu \to x^\mu+dx^\mu \to x^\mu+dx^\mu+\delta{x^\mu} \to x^\mu+\delta{x^\mu}\to x^\mu\)所带来的变化就是两式这差。调整一下求和指标,然后作差,不难得到 \[\begin{align}\label{eq:cedixian8} \Delta{A^\mu}&=-\left(\frac{\partial\Gamma^\mu_{\alpha\gamma}}{\partial x^\beta}-\frac{\partial \Gamma^\mu_{\alpha\beta}}{\partial x^\gamma}+\Gamma^\mu_{\nu\beta}\Gamma^\nu_{\alpha\gamma}-\Gamma^\mu_{\nu\gamma}\Gamma^\nu_{\alpha\beta}\right)A^\alpha dx^\beta\delta{x^\gamma} \notag \\ &=-R^\mu_{\alpha\beta\gamma}A^\alpha dx^\beta\delta{x^\gamma} \end{align}\] 这里 \[\begin{equation}\label{eq:cedixian9} R^\mu_{\alpha\beta\gamma}=\frac{\partial\Gamma^\mu_{\alpha\gamma}}{\partial x^\beta}-\frac{\partial \Gamma^\mu_{\alpha\beta}}{\partial x^\gamma}+\Gamma^\mu_{\nu\beta}\Gamma^\nu_{\alpha\gamma}-\Gamma^\mu_{\nu\gamma}\Gamma^\nu_{\alpha\beta} \end{equation}\] 就是黎曼曲率张量的定义式了,它有4个指标,是一个非常“宏伟”的量。
一句话来说
三种不同的黎曼曲率张量的导出方式,分别从三个角度表明了弯曲空间与平直空间的区别:平直空间中,协变导数的次序是可以交换的,弯曲空间则不是;平直空间中,测地线分布的均匀的、线性的,弯曲空间则不是;平直空间中,一个向量去“溜达”一圈回来之后,并没有变化,而弯曲空间中,向量去“溜达”完之后,可能就不是原来的向量了。