最近学习了蒙特卡罗法，作为尝试使用其算了一下圆周率，感觉大致符合要求。一共写了两个代码，一个是bash脚本，其效率不高，一个是C语言，其效率非常之高可以达到10亿次的运算量，但好像对于改善结果作用不是很明显。
bash版 MCM
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #! /bin/sh
echo "*---------------------------------------*"
echo "| Program: Monte Carlo Method for PI |"
echo "| Version: 1.0 |"
echo "| Author : FengZhenhua |"
echo "| Email : fengzhenhua@mail.bnu.edu.cn |"
echo "*---------------------------------------*"
echo -n "请输入一个统计总数："; read Pi_Total
i=1;Pi=0;Pi_R=0
while [ $i -le $Pi_Total ]
do
random_number=`echo "scale=4 ; ${RANDOM}/32767" | bc -l`
Var_x=$random_number
random_number=`echo "scale=4 ; ${RANDOM}/32767" | bc -l`
Var_y=$random_number
r=$(echo "$Var_x*$Var_x+$Var_y*$Var_y" | bc)
if [ $(echo "$r < 1" | bc) -eq 1 ]; then
let "Pi_R+=1"
fi
let "i+=1"
done
Pi=$(echo "scale=4; 4*$Pi_R/$Pi_Total" | bc)
echo " "
echo "--------------[执行报告]-----------------"
echo " "
echo " 统计时输入的总点数: $Pi_Total "
echo " 位于单位圆内的点数：$Pi_R "
echo " 计算结果：PI=$Pi "
echo " "
echo "-----------------------------------------"
|
将上述代码保存为pi.sh,付与执行权限运行即可。
执行结果
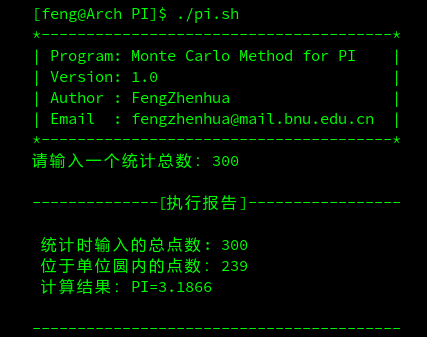Bash版蒙特卡罗法计算PI
C版 MCM
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
void MessageOne()
{
printf("========== Monte Carlo Method For π ==========\n");
printf("*Version: V1.0 *\n");
printf("*Author : FengZhenhua *\n");
printf("*E-Mail : fengzhenhua@mail.bnu.edu.cn *\n");
printf("----------------------------------------------\n");
}
int main()
{
double x;
double y;
double PI;
unsigned long long int r;
unsigned long long int xnum;
unsigned long long int ynum;
unsigned long long int i = 1;
unsigned long long int total = 0;
MessageOne();
printf("\n请输入统计总数：");
scanf("%ld", &total);
srand((unsigned)time(NULL));
while(i <= total)
{
unsigned long long int xnum = rand() % total + 0;
unsigned long long int ynum = rand() % total + 0;
x = (double)xnum/total;
y = (double)ynum/total;
if( x*x+y*y <= 1 )
r++;
i++;
}
PI = (double)4*r/total;
printf("\n-----------------[执行报告]-------------------\n");
printf(" \n");
printf(" 初始输入的统计总点数T: %d \n", total);
printf(" 四分之一单位圆内点数N：%d \n",r);
printf(" 计算公式π=4N/T, 结果：%f \n", PI);
printf(" \n");
printf("----------------------------------------------\n");
return 0;
}
|
将上述代码保存为pi.c,然后执行gcc -o pi pi.c
编译即可。
执行结果
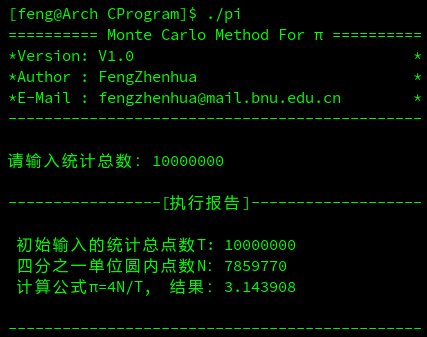C语言版蒙特卡罗法计算PI
祖冲之算法
祖冲之法是用逐次逼近的方法，给出了递推公式，从原理上讲只要计算机算力够用，就可以一直算下去，使结果不断接高精度。同时从最大值和最小值数字相同的位数就可以判断出精确度来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
void MessageOne()
{
printf("=========================== 祖冲之法 For π =======================\n");
printf("*Version : V1.0 *\n");
printf("*Language: C Program *\n");
printf("*Author : FengZhenhua *\n");
printf("*E-Mail : fengzhenhua@mail.bnu.edu.cn *\n");
printf("------------------------------------------------------------------\n");
}
int main()
{
double SideLength=1;
double PI_min;
double PI_max;
unsigned long long int n=6;
int n_max=0;
unsigned long long int i=0;
PI_min=3;
MessageOne();
printf("\n请输入正多边形的边数因子[边数=6*2^n]：n= ");
scanf("%d", &n_max);
while(i < n_max)
{
n=2*n;
SideLength=(double)sqrt(2-sqrt(4-SideLength*SideLength));
PI_min=(double)PI_min+n*SideLength*(1-sqrt(1-SideLength*SideLength/4))/2;
PI_max=(double)PI_min+n*SideLength*(1-sqrt(1-SideLength*SideLength/4))/2;
i++;
}
printf("\n---------------------------[ 执行报告 ]---------------------------\n");
printf(" \n");
printf(" 正多形边数N: %ld \n", n);
printf(" π 的下限Min：%.49f \n",PI_min);
printf(" π 的上限Max：%.49f \n",PI_max);
printf(" \n");
printf("------------------------------------------------------------------\n");
return 0;
}
|
将上述代码保存为cpi.c,然后执行gcc -o cpi cpi.c -lm
编译即可,其中选项-lm是因为在linux中gcc不包括标准库math.h，使用此选项可以使其连接到库math.h。
执行结果
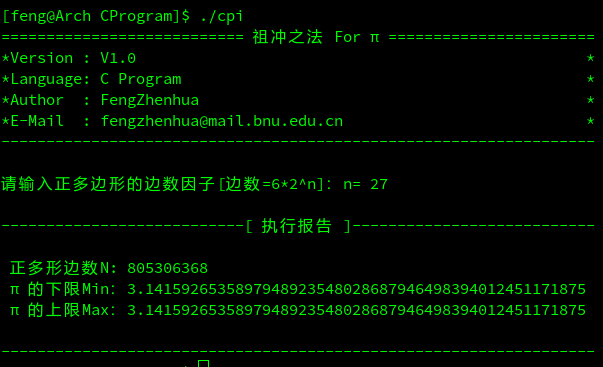C语言版祖冲之法计算PI
微积分算法
2022-10-23
使用微积分定义实现圆周率的计算，此法原则是一个通用的计算定积分的方法，但是在电脑上执行情况来看效率不见得高。因为在分割十亿次的分割后才能确定圆周率的范围
3.1415926到3.1415927之间。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
#include <stdio.h>
#include <math.h>
void MessageOne()
{
printf("=========================== 微积分法 For π =======================\n");
printf("*Version : V1.0 *\n");
printf("*Language: C Program *\n");
printf("*Author : FengZhenhua *\n");
printf("*E-Mail : fengzhenhua@mail.bnu.edu.cn *\n");
printf("------------------------------------------------------------------\n");
}
int main()
{
unsigned long long int n;
unsigned long long int i;
double h_min=0;
double h_max=0;
double PI_min;
double PI_max;
MessageOne();
printf("\n请输入自变量x的分割段数：n= ");
scanf("%d", &n);
while( i < n )
{
h_max=(double)h_max+sqrt(n*n-i*i)/n;
i++;
}
h_min=h_max-1;
PI_max=4*h_max/n;
PI_min=4*h_min/n;
printf("\n---------------------------[ 执行报告 ]---------------------------\n");
printf(" \n");
printf(" 自变量分割段数: %ld \n", n);
printf(" π 的下限Min：%.49f \n",PI_min);
printf(" π 的上限Max：%.49f \n",PI_max);
printf(" \n");
printf("------------------------------------------------------------------\n");
return 0;
}
|
执行结果
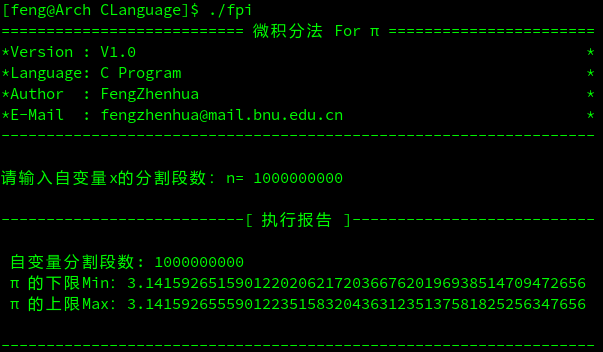C语言版微积分法计算PI